

MILIEU.
Expeditions in Digital Technologies
Tutors: Jinal Shah, Santdeep Kaur

A gyroid is a triply periodic minimal surface with zero mean curvature, discovered by Alan Schoen in 1970. It features a smooth, continuous, and non-self-intersecting structure with no straight lines or planar symmetry. Known for its intricate, maze-like geometry, the gyroid is valued for its strength, lightweight properties, and efficient material distribution, making it ideal for applications in architecture, aerospace, filtration, and 3D printing.
<
Initial Models
>
<
Other Initial Explorations
>

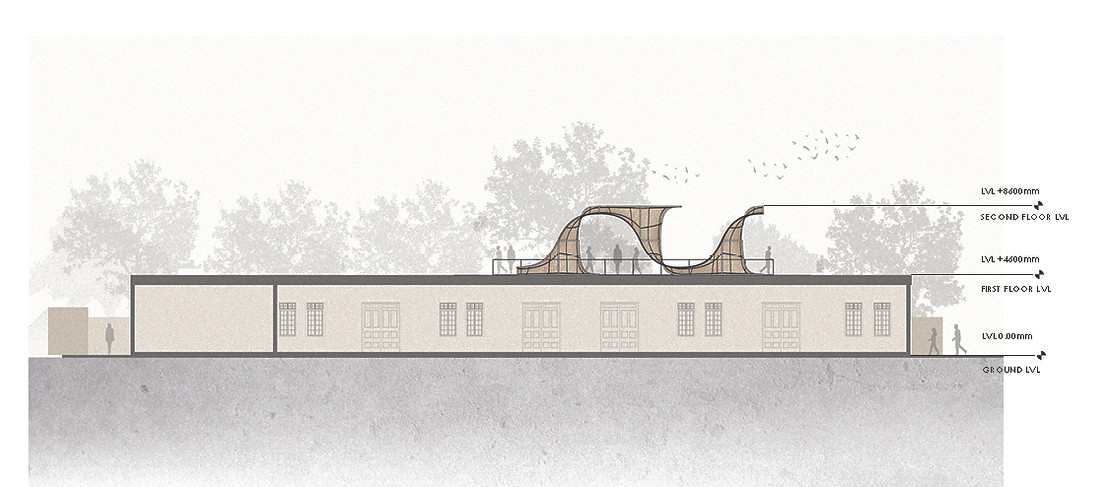
Breaking down gyroids into modules involves isolating a single repeating unit of the complex surface, which can be replicated to form the entire lattice structure. This process focuses on defining and refining this unit module in 3D geometry, ensuring it aligns seamlessly when multiplied, ultimately recreating the gyroid's intricate and continuous pattern.

This project explores gyroids, minimal surfaces with zero mean curvature, to create an adaptable informal workspace. By breaking the gyroid into its smallest unit module, the design forms versatile structures with interspaces for lounging, sitting, and creative use. The arrangement balances division and continuity, resulting in an experiential and accommodating environment.

PLAN
SECTION
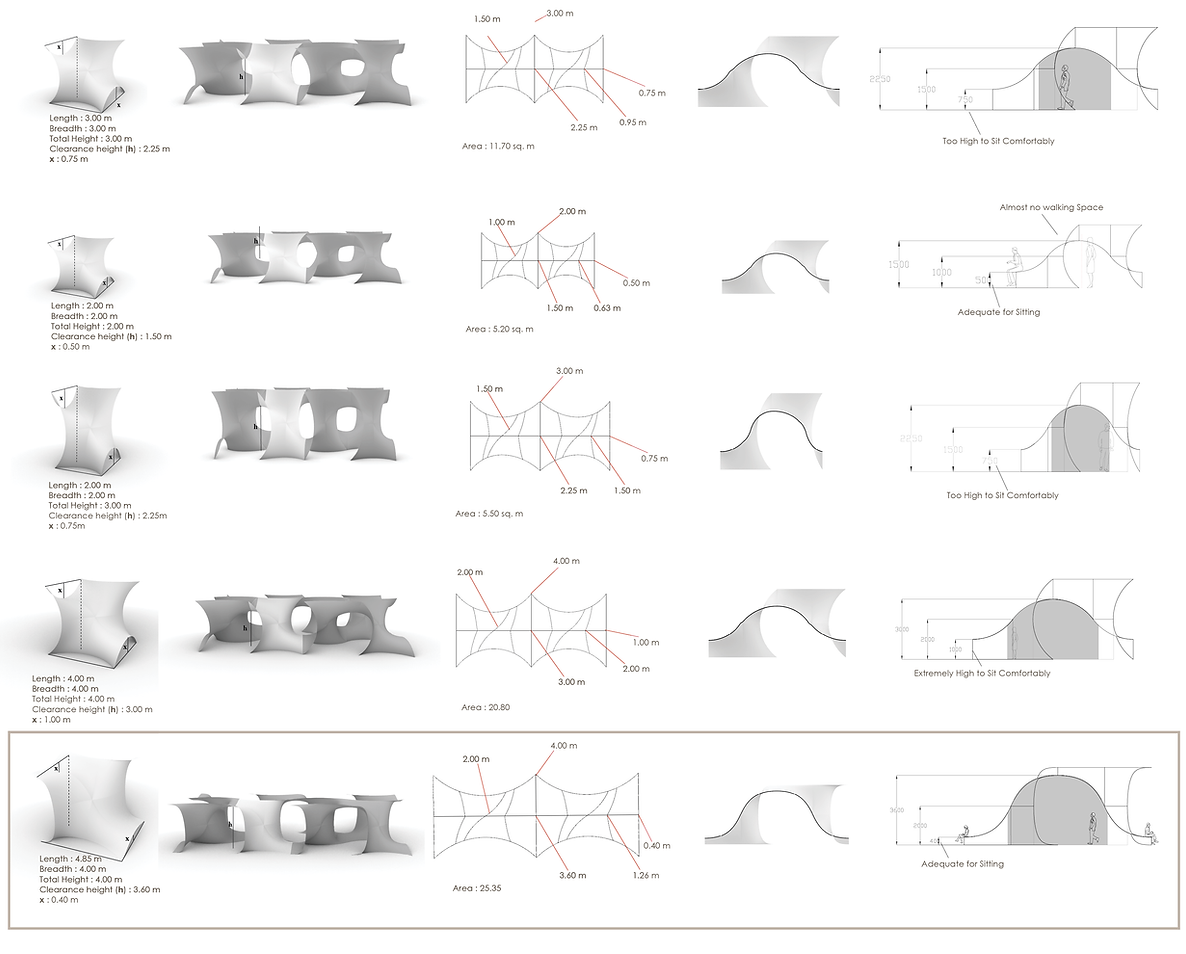
Experimenting with varying dimensions of the bounding box of the gyroid and seeing what aligns best anthropometrically
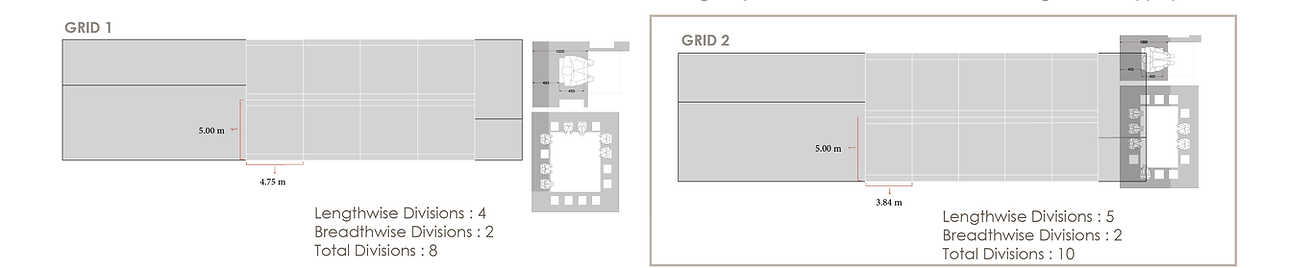
The sight and the spatial divisions on the plan
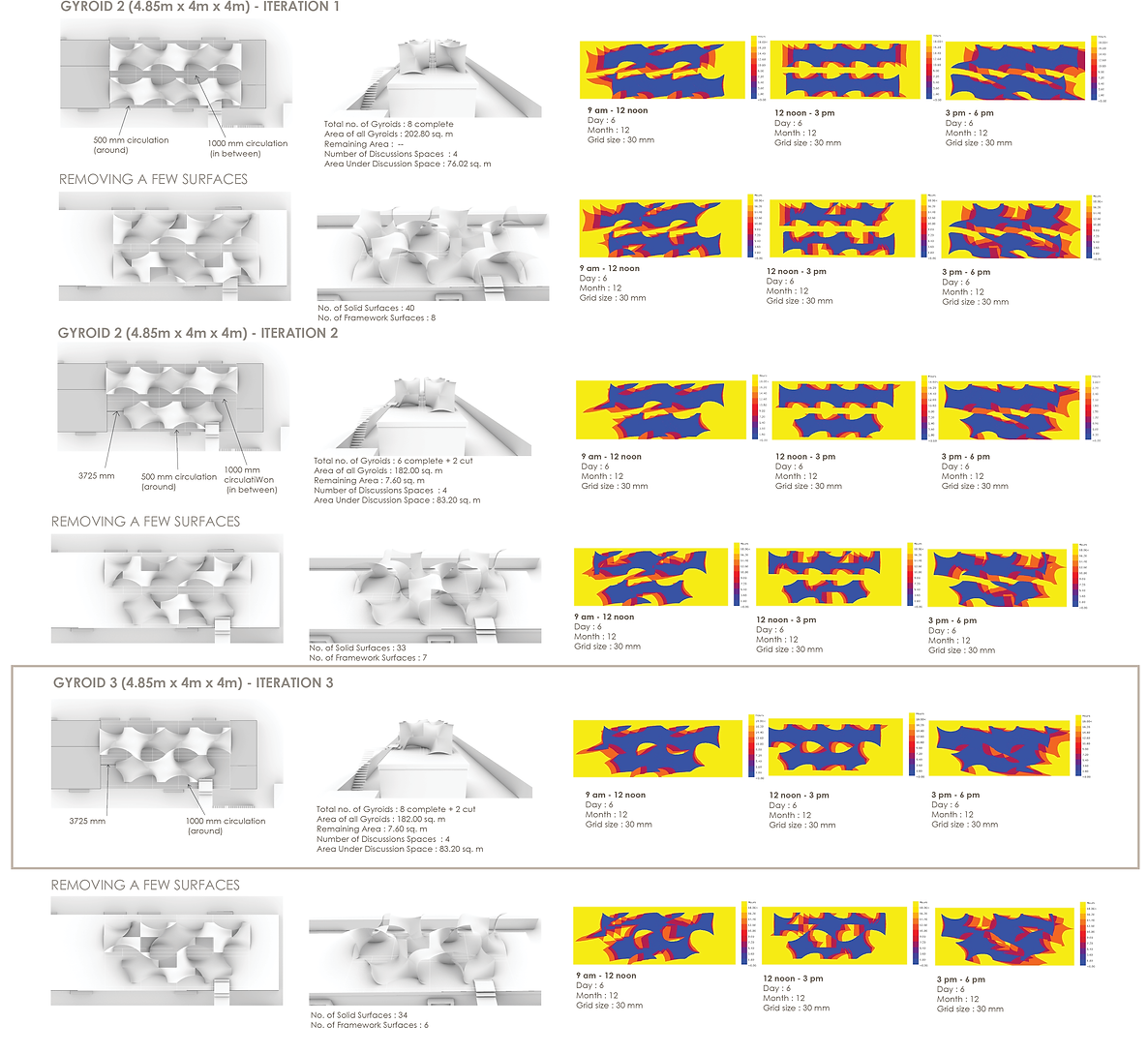
Looking at various arrangements of selected gyroids. Selecting an ideal arrangement based on sunlight analysis
<
The Space - with Cane as the Building Material
>
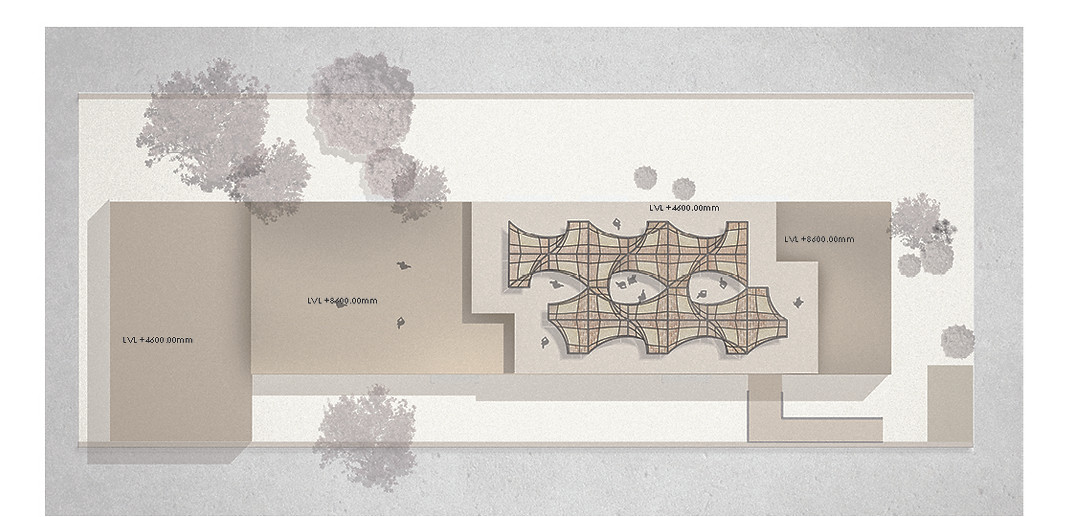
<
Scaled Models and Weaves
>



